Introduction

Lorsque Rennes et Nantes décideront des stratégies pour développer leurs aéroports, les choix vont s’élaborer à partir d’une confrontation, plus ou moins explicite, de deux types d’intérêts. La recherche d’un intérêt personnel le plus élevé pourra prévaloir qui consistera essentiellement à capter le maximum de ressources générées par l’infrastructure sans se préoccuper de la situation de l’autre ville. Elle est a priori la conduite la plus prévisible pour un acteur institutionnel évoluant dans un contexte de concurrence territoriale exacerbée. À l’opposé, les deux villes peuvent choisir un mode de gouvernance coopératif qui privilégie l’intérêt collectif. Dans ce cas, elles devront se concerter préalablement pour décider des stratégies à mettre en place ainsi que du partage des bénéfices. Ce mode de gouvernance n’est pas sans difficulté. Il oblige les acteurs à abdiquer une partie de leur pouvoir de décision au profit d’une instance collective. La coopération soulève également la question de la confiance entre les individus. Dans cet article, nous allons rappeler quelques éléments constitutifs de ce débat déjà ancien, en soulignant que les intérêts individuels et collectifs sont parfois divergents et souvent inconciliables. Nous verrons également comment les concepts de la théorie des jeux ont permis de renouveler les thèses de cette controverse. Un second article examinera les principaux enseignements à tirer pour Nantes et Rennes en termes, notamment, de gouvernance aéroportuaire.

1. De la conception harmonieuse des classiques au dilemme du prisonnier

Le principe de la « main invisible » d’Adam Smith

En proposant le principe de la « main invisible », Adam Smith (1776) pensait concilier l’intérêt collectif et l’intérêt individuel. Pour l’économiste écossais du XVIII^e siècle, l’intérêt général n’est pas le résultat de la bonne volonté du souverain ou de l’action éclairée de l’État. C’est, au contraire, dans le commerce entre les individus fondé sur la poursuite des intérêts égoïstes de chacun qu’il doit naturellement émerger.

Ce n’est pas de la bienveillance du boucher, du boulanger ou du marchand de bière dont nous attendons notre dîner, mais bien du soin qu’ils apportent à leurs intérêts. Nous ne nous adressons pas à leur humanité, mais à leur égoïsme ; et ce n’est jamais de nos besoins que nous leur parlons, c’est toujours de leur avantage.

Empruntant le thème original chez Bernard de Mandeville et sa Fable des abeilles (1704), la métaphore de la main invisible suggère que les « vices privés » se transforment en « vertus publiques » (Perrot, 1984). L’économie doit alors prendre pour point de départ, les comportements des individus poussés par leur égoïsme naturel. La liberté individuelle, qui est une conséquence de ce principe, consiste pour chacun à choisir la meilleure façon d’accroître son intérêt personnel sans se soucier du bien commun.

En dirigeant cette industrie de manière que son produit ait le plus de valeur possible, il ne pense qu’à son propre gain ; en cela, comme dans beaucoup d’autres cas, il est conduit par une main invisible à remplir une fin qui n’entre nullement dans ses intentions ; et ce n’est pas toujours ce qu’il y a de plus mal pour la société, que cette fin n’entre pour rien dans ses intentions.

La conception smithienne de l’intérêt général repose sur le mécanisme de la main invisible qui oriente les décisions individuelles vers l’optimum collectif. Elle constitue une véritable philosophie économique dans laquelle le marché devient l’outil de résolution des problèmes que l’État et le politique ont été jusque là impuissants à régler (Rosanvallon, 1989). Les économistes qui vont poursuivre le travail d’Adam Smith vont, notamment les économistes de l’école de Lausanne (Walras et Pareto), systématiser la notion de main invisible. Confondue au mécanisme des prix, la main invisible doit conduire, dans un système de marchés concurrentiels, à l’équilibre économique. Le système s’autorégulant, le rôle économique de l’État est alors naturellement limité par l’ordre spontané du marché.

L’optimum de Pareto

Dans son « Manuel d’économie politique » publié en 1906, Vilfredo Pareto (1848-1923) va approfondir et généraliser le principe d’Adam Smith. Il propose sous le nom de maximum d’ophélimité ou optimum de Pareto (terme consacré par l’usage), un concept qui permet de définir un optimum économique pour une société. Pareto part du principe qu’une affectation des ressources est préférable à une autre si elle est préférée par tous les membres qui composent la collectivité. La comparaison des différentes affectations possibles des ressources dans une économie conduit à déterminer l’optimum de Pareto qui correspond à une situation dans laquelle on ne peut améliorer la situation de certains individus sans détériorer celle d’autres. Il n’y a donc pas de gaspillage de ressources. Malgré ses limites, ce concept permet d’indiquer, parmi un ensemble de situations possibles, celles qui sont non-optimales.

La notion de « main invisible » des marchés a été à l’origine d’une abondante littérature. Associée à la notion d’optimum de Pareto, elle constitue un des fondements de la construction théorique de la microéconomie, notamment en ce qui concerne le modèle de concurrence parfaite. Les deux théorèmes de l’économie du bien-être montrent que l’équilibre concurrentiel est un optimum de Pareto (Guerrien, 2002). Que cet équilibre correspond à la meilleure allocation des ressources possibles et qu’il s’agit d’un état efficient de l’économie. D’où le caractère souvent normatif des travaux des théoriciens qui cherchent la manière la plus appropriée pour l’atteindre et qui transforment ce critère en une norme censée représenter l’état d’équilibre économique idéal.

Le dilemme du prisonnier : un « antithéorème de la main invisible »1

Depuis Adam Smith et Vilfredo Pareto, la science économique a progressé, notamment en ce qui concerne la connaissance des défaillances des marchés et les problèmes posés au principe de la main invisible par l’existence des externalités et des biens publics. Les comportements des agents économiques vont en être nécessairement affectés. Alors que dans le cadre de la concurrence parfaite, ces agents n’ont pas de stratégie à élaborer car les prix sont donnés et les actions des uns n’ont pas d’influence sur les autres, les imperfections du marché vont favoriser les interactions stratégiques entre eux. Il devient alors primordial pour les agents d’être capables d’anticiper les actions des autres et d’agir en conséquence. La théorie des jeux, qui étudie ces interactions, va mettre en évidence les difficultés que les agents économiques ont à se coordonner.

C’est ainsi que le principe de la main invisible a été remis en cause, avec notamment l’apport des théoriciens des jeux qui ont montré que la confrontation des intérêts individuels ne débouche pas nécessairement sur l’optimum collectif (Pareto). Le modèle de base qui illustre les limites du principe de la main invisible est celui du dilemme du prisonnier. Ce modèle, proposé en 1950 par les mathématiciens de la Rand Corporation, Melvin Dresher et Merrill Flood, et formalisé par Albert Tucker, attire l’attention sur le fait que la poursuite de l’intérêt personnel peut conduire à une situation sous-optimale au sens de Pareto.

Le dilemme du prisonnier peut être illustré de la façon suivante : deux bandits sont arrêtés et isolés. Les enquêteurs n’ont pas suffisamment d’éléments pour les condamner. On leur propose, séparément, de coopérer avec la police en dénonçant le partenaire. Celui qui coopère est relâché, tandis que l’autre écope de plusieurs années d’emprisonnement. Si aucun ne dénonce l’autre, ils subiront une faible peine. Aucune communication entre les deux prisonniers n’est possible.

Matrice 1 : illustration d’un dilemme du prisonnier

	Bandit 2	Se taire (S3)	Dénoncer (S4)
Bandit 1
Se taire (S1)		(-1, -1)	(-6, 0)
Dénoncer (S2)		(0, -6)	(-4,-4)

Ce dilemme met en évidence que, quelle que soit l’attitude de son complice, chacun des prisonniers a intérêt à dénoncer l’autre. Les stratégies adoptées seront le couple (S2, S4) qui n’est pas un optimum de Pareto. Ce choix rapporte collectivement (–8) alors que le couple de stratégies (S1, S3) rapporte (–2). Ce dilemme illustre le conflit entre l’intérêt individuel qui dicte de dénoncer son complice et l’intérêt collectif qui consiste à se taire. Le résultat est le même si le jeu est joué une fois ou un nombre fini de fois. Le principe du raisonnement par récurrence à rebours2 conduit alors les joueurs à rester prisonniers du dilemme du prisonnier. Seuls les cas d’un jeu répété indéfiniment ou d’un jeu dont la fin n’est pas connue des joueurs ouvrent des perspectives de coopération car le dernier coup du jeu n’étant pas calculable, le raisonnement par récurrence à rebours n’est pas possible (Axelrod, 1984).

L’équilibre de Nash

Le couple de stratégies (S2, S4) correspond à l’équilibre de Nash (1950) du jeu car aucun joueur ne regrette son choix après avoir constaté celui des autres joueurs. Un équilibre de Nash est un ensemble de stratégies (une par joueur) tel qu’aucun joueur ne peut obtenir un gain supplémentaire en changeant unilatéralement de stratégie sous peine d’être immédiatement placé, au vu des stratégies retenues par l’autre joueur, dans une situation plus mauvaise. Il correspond à l’issue logique du jeu lorsque les joueurs se comportent de façon rationnelle.

Dans l’exemple du dilemme du prisonnier, si l’un des deux prisonniers décide de se taire, il sera immédiatement sanctionné (sa peine passera de quatre à six ans tandis que l’autre joueur sera libéré). Et c’est là que réside le dilemme car l’équilibre de Nash est sous-optimal au regard du critère de Pareto. En outre, le fait qu’un joueur ne puisse changer unilatéralement de stratégie pour sortir d’un équilibre de Nash sous optimum résulte de l’absence de coopération. Cela conduit les individus, dans certains cas, à choisir une solution qui correspond à un gaspillage des ressources. Aussi, la problématique associée au dilemme du prisonnier est-elle tout autre que celle de l’économie classique. Il ne s’agit plus d’améliorer le fonctionnement du marché pour rendre les échanges plus efficaces. La question fondamentale est : comment faire émerger la coopération entre les individus pour éviter des situations d’équilibre de Nash sous-optimales afin d’atteindre l’optimum de Pareto (gain collectif le plus élevé) ?

2. Comment être efficace dans un dilemme du prisonnier ?

Coopération et réciprocité : les simulations informatiques d’Axelrod

Robert Axelrod a beaucoup travaillé sur le dilemme du prisonnier dans les années 1980 en organisant des tournois informatiques dans lesquels les joueurs confrontaient des programmes qui simulaient différentes stratégies. Comme la version classique en un coup du dilemme du prisonnier ne donne aucune perspective de coopération, le jeu est répété un nombre inconnu de fois. Dans ce cas, le jeu est dit itéré. Ne sachant quand la partie va se terminer, il est alors possible d’étudier la stratégie des joueurs afin de déterminer celle qui est la plus adaptée.

La stratégie de coopération conditionnelle « Tit-for-Tat » ou donnant-donnant proposée par Anatole Rapoport allait marquer sa supériorité sur toutes les autres. La stratégie « Tit-for-Tat » qui est d’une grande simplicité, consiste à débuter la partie en coopérant et à répéter le coup précédent de l’autre joueur. Finalement, à partir du deuxième coup, cette stratégie consiste à coopérer si le partenaire coopère et à cesser immédiatement la coopération dès qu’il fait cavalier seul. Enfin, si le partenaire souhaite reprendre la coopération, la stratégie « Tit-for-Tat », qui n’est pas rancunière, adopte la même attitude. La particularité de « Tit-for-Tat » est qu’elle ne gagne jamais une partie d’un tournoi.

Cette stratégie ne peut battre aucun autre programme dans une confrontation directe car le seul moyen de remporter un match est faire « cavalier seul » plus souvent que l’autre, ce qui est impossible avec donnant-donnant. Autrement dit, donnant-donnant ne gagne aucun match mais remporte le classement final avec le gain total le plus élevé. Axelrod explique ce paradoxe par le fait que les autres programmes, moins coopératifs et plus agressifs, réduisent considérablement les gains de chacun des joueurs à chaque fois qu’ils sont confrontés les uns aux autres, y compris à des programmes identiques aux leurs.

Promouvoir la coopération selon la stratégie « Tit-for-Tat »

À partir des enseignements de la stratégie « Tit-for-Tat », Robert Axelrod préconise principalement trois types de mesures afin de favoriser la coopération dans les relations sociales.

La « Tit-for-Tat » attitude

• Il convient de ne pas être trop envieux (première règle), l’essentiel étant d’engranger des gains, sans qu’il soit nécessaire que ceux-ci soient supérieurs à ceux de l’autre joueur, mais simplement supérieurs à ceux issus d’un comportement de cavalier seul. Dans ce sens, Axelrod rappelle qu’il est inutile d’« être jaloux du succès d’un autre joueur, car, dans un dilemme du prisonnier itératif de longue haleine, la réussite de l’autre est une condition sine qua non de votre réussite ».
• La deuxième règle recommande de ne jamais être le premier à faire cavalier seul, afin de ne pas s’exposer à la riposte de son adversaire et de laisser la voie ouverte à une entente réciproque.
• La troisième règle postule de pratiquer la réciprocité dans la coopération comme dans la défection. La susceptibilité est une des caractéristiques de « Tit-for-Tat » qui répond par la défection immédiatement après que l’autre joueur a fait défection et qui reprend la coopération aussitôt que le joueur joue la coopération.
• Enfin, la quatrième règle recommande qu’il n’est pas nécessaire d’être trop malin en élaborant des stratégies complexes car il ressort des simulations informatiques qu’elles ne font pas mieux que les autres.

Le poids accordé à l’avenir

Au-delà de ces attitudes propices au développement de la coopération, Axelrod recommande d’« augmenter l’ombre projetée par l’avenir sur le présent » afin d’infléchir les comportements opportunistes. Si les joueurs accordent une valeur élevée à l’avenir, le montant futur actualisé des gains de la coopération sera supérieur au gain immédiat de la défection. Il convient alors de privilégier les relations durables et de multiplier la fréquence des échanges afin d’accroître le poids de l’avenir. Ces éléments sont pour Axelrod indispensables pour rendre stable la coopération.

Ce qui rend la coopération possible, c’est le fait que les joueurs peuvent être amenés à se rencontrer à nouveau. Cela signifie que les choix effectués aujourd’hui déterminent non seulement le résultat du coup présent, mais peuvent également influencer les choix ultérieurs des joueurs. L’avenir peut donc projeter son ombre sur le présent et affecter ainsi la situation stratégique actuelle.

La modification des gains des joueurs

Axelrod propose une troisième solution pour favoriser la coopération dans le cadre d’un dilemme du prisonnier répété. Elle consiste à intégrer dans le calcul le coût non-financier de la non-coopération. À l’issue de cette modification des gains, les incitations des joueurs changent et la stratégie de défection ne représente plus nécessairement le seul équilibre de Nash du jeu.

Les critiques de la coopération sans confiance d’Axelrod

Selon Axelrod, la coopération trouve son explication dans la pratique de la réciprocité dont la stratégie donnant-donnant est l’archétype et dans l’importance accordée à l’avenir. La confiance n’est pas nécessaire à la coopération.

La pierre angulaire de la coopération est plus la durabilité des rapports que la confiance. […] Que la confiance règne ou non entre les joueurs est moins important à long terme que le fait que les conditions soient propices à la construction d’un mode de coopération stable entre eux.

Cette thèse de la coopération sans confiance a suscité une vive controverse.

Certaines critiques réfutent l’idée que la coopération puisse apparaître sans un minimum de confiance (Gambetta, 1988). Reprenant l’analyse d’Axelrod sur le système « vivre et laisser vivre » entre les combattants pendant la première guerre mondiale (Ashworth, 1980), Gambetta conteste l’explication d’Axelrod sur l’évolution de la coopération uniquement à partir de la proximité et de la durée des hostilités. Il montre qu’une telle attitude n’a pu se développer que parce que les soldats étaient disposés à « faire confiance à la confiance ». D’autres critiques abordent le problème de la continuité de la coopération en l’absence de confiance. L’étude de Gulati et al. (1994) sur les accords d’entreprises souligne que la stratégie donnant-donnant est souvent utilisée par les dirigeants. Elle montre, cependant, qu’une application stricte de donnant-donnant dans les affaires, notamment en ce qui concerne l’usage de la susceptibilité est contre-productif. Elle conduit le plus souvent à des mesures de représailles réciproques qui marquent la fin de la coopération. Par ailleurs, l’absence totale de rancune semble également peu adaptée. Cela peut renforcer le comportement opportuniste entre les individus et conduire à une instabilité de la coopération.

Si ces études montrent l’importance de la durée des échanges et des perspectives d’avenir pour comprendre la coopération entre les individus et en ce sens confirment l’apport d’Axelrod, elles soulignent également que l’analyse proposée par ce dernier ne fournit pas une explication complète de la coopération. Par conséquent, si la confiance est au cœur de la problématique de la coopération, elle peut faire elle-même l’objet d’une analyse. Nous nous bornerons ici à présenter quelques éléments issus de la théorie des jeux sur la formation de la confiance, depuis le travail précurseur de M. Deutsch ainsi que le modèle de D.M. Kreps qui fait référence aujourd’hui.

La confiance et la loyauté : l’apport de Morton Deutsch

Le psychologue Morton Deutsch a réalisé à la fin des années 50 une série d’expérimentations auprès de ses étudiants afin de comprendre la psychologie des individus face à un dilemme du prisonnier (Deutsch, 1958). Le jeu proposé par Deutsch est séquentiel avec information parfaite, c’est-à-dire que les joueurs décident l’un après l’autre, le second connaissant le choix du premier au moment de jouer. Les joueurs disposaient de deux stratégies : coopérer ou trahir. À chaque stratégie, Deutsch associait un comportement particulier. Pour le joueur qui joue en premier, la coopération traduit une attitude de confiance par rapport à l’autre joueur. À l’inverse, la trahison correspond à de la suspicion.

Pour le second, jouer la confiance lorsque le premier a choisi de coopérer traduit la loyauté, alors que s’il joue la trahison sa décision correspond à un manque de loyauté. La matrice suivante présente le jeu séquentiel proposé par M. Deutsch (1958).

Matrice 2 : jeu séquentiel

	Joueur 1	Coopérer	Trahir
Joueur 2
Coopérer		(+9, +9)	(-10, +10)
Trahir		(+10, -10)	(-9, -9)

Le jeu a été proposé à 55 étudiants de psychologie. Les résultats font apparaître une forte corrélation entre les comportements « être confiant » et « être loyal ». Autrement dit, les joueurs qui font confiance quand ils jouent en premier adoptent généralement une attitude loyale lorsqu’ils jouent en second. Tandis que les joueurs qui, en premier, choisissent de trahir adoptent une attitude déloyale lorsqu’ils jouent en second. Ce résultat, confirmé par de nombreux auteurs, montre comme le note Nicolas Eber (2004) que les individus se comportent moins selon le principe moral « faites aux autres ce que vous voudriez qu’ils vous fassent » que selon le principe cognitif « faites aux autres ce que vous pensez qu’ils vont vous faire, et attendez-vous à ce qu’ils vous fassent ce que vous leur aurez fait ».

Deutsch a également comparé les résultats obtenus par un groupe où les joueurs ne communiquaient pas, avec un autre dans lequel, suivant ses instructions, les joueurs décrivaient ou étaient informés, partiellement ou complètement, de la nature des interactions. Les informations transmises révélaient les intentions d’un joueur ainsi que ses attentes vis-à-vis de l’autre joueur. Elles décrivaient également le système de sanctions appliquées en cas de trahison et la conduite à tenir pour réparer une éventuelle défection. Le résultat de l’expérience montre que le comportement coopératif est plus élevé dans le groupe où les joueurs ont pu bénéficier d’une information complète que dans le groupe privé de communication. Deutsch en tire la conclusion que la confiance peut se développer entre des individus à la condition que la communication permette d’expliciter quatre éléments qui sont : l’attente et l’intention (expectation and intention) du joueur qui donne sens à la relation et qui clarifie les comportements, la rétorsion et l’absolution (retaliation and absolution) qui définissent le système de sanctions en cas de non-respect des attentes et la conduite à tenir pour réparer tout manquement et retrouver une démarche coopérative.

Les conclusions de Morton Deutsch sur le rôle de la confiance dans la coopération sont éloignées de celles d’Axelrod. Elles montrent que la confiance et la loyauté entre les individus sont étroitement liées et qu’elles jouent un rôle déterminant dans l’établissement d’une coopération durable. Elles soulignent également l’importance d’informer le partenaire sur les quatre éléments nécessaires pour une coopération durable (attente, intention, sanction et absolution), et en particulier, de lui communiquer la démarche utilisée pour absoudre une défection. Les résultats de ces expériences montrent également que la confiance permet de faire preuve d’indulgence. Alors que pour Axelrod toute défection doit être immédiatement sanctionnée (susceptibilité absolue de « Tit-for-Tat »), Deutsch, au contraire, recommande de faire preuve de tolérance face aux défaillances mineures du partenaire afin d’éviter le risque d’entrer dans une spirale de sanctions qui marquerait la fin de la coopération. La tolérance pouvant être définie comme le degré avec lequel une des parties en présence accepte de poursuivre la coopération malgré le fait qu’un partenaire ait manqué à ses obligations.

La confiance et la réputation : l’apport de David M. Kreps

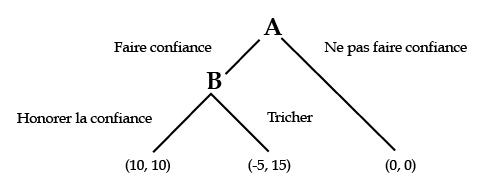
L’intérêt de la réflexion de D. Kreps (1990) est de considérer que la confiance est le résultat d’un calcul rationnel (économique) qui repose sur la réputation des joueurs. Le modèle développé est une variante du dilemme du prisonnier séquentiel que Kreps appelle « jeu de la confiance ». Dans ce jeu, le joueur A dispose de deux stratégies : accorder sa confiance ou ne pas l’accorder à un joueur B. B répond à la décision de A en choisissant de coopérer ou de trahir la confiance. L’arbre du jeu de la confiance de Kreps est le suivant :

Lorsque le jeu est joué une seule fois, la seule issue rationnelle pour A est de ne pas accorder sa confiance au joueur B. Pour vérifier ce choix, on procède selon la méthode de l’induction à rebours qui consiste à déterminer le meilleur choix du joueur B puis à considérer le choix du joueur A. Ainsi, de manière rationnelle, le joueur B ne peut choisir que de tricher car cela lui procure un gain de 15 contre un gain de 10 s’il honore la confiance de A. Anticipant le comportement de B, le joueur A choisit de ne pas faire confiance. C’est le seul équilibre de Nash du jeu. Cependant, en l’absence d’échange, les deux joueurs se privent des gains qu’ils auraient pu obtenir avec la coopération. La situation n’est donc pas Pareto optimale.

Dans le modèle de Kreps, le jeu est répété un nombre fini de fois avec, à chaque étape, une probabilité élevée pour qu’il se poursuive encore au moins un tour. Concrètement, le joueur B est amené à rencontrer à chaque nouvelle occurrence d’autres joueurs A2, A3, etc., (noté Ai). Par principe, les joueurs Ai n’accordent leur confiance qu’à des joueurs B jouissant d’une bonne réputation. Si B a décidé d’honorer la confiance d’un A lors du tour précédent, sa réputation est intacte et le nouveau joueur Ai va accepter de lui faire confiance. Par contre, dès l’instant où B a triché au moins une fois, sa réputation est définitivement souillée et plus aucun joueur Ai ne souhaitera entrer en relation avec lui. Par conséquent, si le jeu est répété un nombre indéfini de fois, B a intérêt à toujours honorer la confiance de A. C’est la seule stratégie qui lui offre l’assurance de poursuivre dans l’avenir les échanges avec les autres joueurs Ai et de bénéficier des gains de la coopération.

Dans l’approche de Kreps le mécanisme de la réputation est suffisant pour assurer la pérennité de la coopération entre les joueurs A et B. Il est plus efficace qu’un contrat formel car il ne supporte aucun coût de transaction pour assurer son application. La réputation s’acquiert et n’est jamais donnée d’emblée.

Elle constitue un actif spécifique pour le joueur qui conserve sa valeur pendant tout le temps qu’il honore la confiance de son partenaire. L’intérêt de ce modèle est d’expliquer la formation de la confiance à partir des décisions rationnelles des joueurs fondées sur la maximisation des gains.

Conclusion

L’objectif de cette présentation était de rappeler un certain nombre de concepts issus notamment, de la théorie des jeux qui jalonnent le débat sur le rapport entre l’intérêt individuel et collectif. Nous montrerons, dans un prochain article, que ces concepts peuvent enrichir la réflexion sur le choix des différentes stratégies aéroportuaires dans le cas de Nantes et Rennes.